My Surly Cross-Check was showing its age. My philosophy with bikes, as with most of life, is to use things until they break, and then to keep on using them, until they've broken multiple other things. “Unrideability” is my criterion for replacement, or even for basic maintenance.

In fifteen thousand miles I had not changed the chain once. It wasn't a huge deal. The chain had stretched a bit—all those rotations wear away at the pins holding the links together, micron by micron—but it still rode well and only slipped if I was really trying to book it up a steep hill in a high gear.
Then the chain broke. I installed a new one, but I may as well have given a heart transplant to a ninety-year-old. It just didn't work. The stretched chain had worn the gear teeth down to daggers, and now that I had a new, normal-sized chain, it no longer fit into the freakishly-large gaps. If I was in the very lowest gears, I could pedal successfully, but if I tried to do anything higher, the chain slipped. And slipped is too generous a word: it rattled over every tooth, barely rotating the wheel. It reminded me of driving up a hill in Quebec once during an ice storm: the speedometer said 60 mph, but the slow passage of the scenery said 5 mph.
I needed not just a new chain. I needed new gears.
Along with air-filled tires, gears were one of the crucial elements that turned bicycles from an engineering curiosity to a functional tool. In the old days of penny farthings, there was no such thing as a gear on a bicycle. Every time you rotated the pedals once, the wheel rotated once. In effect, the only way you could go faster or go slower was to pedal faster or pedal slower.
But everyone who rides a bike knows that pedaling really fast sucks, and pedaling really slow is painful. You want to pedal at a more-or-less constant rate—you want the time it takes you to make one pedal revolution to not always be the same time it takes the wheel to make one revolution. Gears let you do this. Gears are like pulleys—but for rotational rather than linear motion.
Say I'm on my Cross-Check, and I'm in the gear combination with the front 48-toothed gear and the rear 16-toothed gear. If I turn the pedals once, what happens? The front gear, with 48 teeth, goes around once, and so the chain advances by 48 links. The rear gear, however, doesn't know or care how many times the front gear has gone around—it only cares about how much the chain wants it to move. The chain has advanced by 48 links, and so the rear gear rotates by 48 teeth. But since the rear gear only has 16 teeth, this means that the rear gear has to rotate three times (because 48/16 = 3. This is where the fancy word “gear ratio” comes in: your gear ratio, in this case, is 3.) So in the 48/16 combination, you rotate the pedals once, and your rear wheel goes around thrice.
But suppose you're in a slightly different gearing. Say you're using a smaller chainring in front, with 36 teeth, and you're using a smaller cog, too, with 12 teeth. This works out to being exactly the same as the 48/16 combination: every time you rotate the pedals once, the rear wheel turns three times. (36/12 is also 3.) Of course it's not THE SAME the same: they're totally different gears. The effect on your pedaling is the same, but your shifters are in a different position and your chain is touching different teeth.
In non-financial ways, the fact I needed to replace my entire drivetrain was a welcome development. I had bought the bike in Chicago, but now I live in San Francisco. The gears that had been nice on Halsted Street were knee-breakers on Nob Hill. I had toyed with the idea of adding a “granny gear”—a third, smaller front gear to help with hills—and this was my chance.
But as soon as I started looking at options, I faced all the paralysis of staring down 500 different kinds of peanut butter in the supermarket. Do I get a nice Tiagra road triple, with 50-39-30-toothed gears in the front? That's lower than my current drivetrain, and a bit higher—I'd be able to go up steeper hills, and on the flatlands I'd be able to faster. Or do I get a Deore mountain triple, with 48-36-26-toothed front gears? That gearing is way lower, so I'd be able to go up even steeper hills. (Twin Peaks, here I come!) But it's not any faster than what I already had. Am I happy with how fast I can currently go on the flatlands? And what about in between? I was only thinking about the extreme highest and lowest gears—the “edge cases,” as my programmer friends say, or the “marginal cases,” as my economist friends say. These thoughts racked my brain as I stared at the metaphorical wall of peanut butter. (Which in this case was actually the Shimano website.)

How do you choose what gearing to get? Do you just calculate all the gear ratios and ponder them? What's the best way to think about gearing? If you Google “bike gear analyzer” or the like, you can find all sorts of online calculators that claim to help. They take in your gearing and spit out tables and tables of numbers: gear ratios, gain ratios, speed, splits, meters development, gear inches. I don't know what half of these things mean. Even if I did, I doubt that looking at a giant table of numbers would suddenly make me understand how my bike works. It seems, as Edward Tufte has argued, that the best way to represent huge amounts of numerical data is with pictures. Would you rather have a list of the closing prices of the New York Stock Exchange every day for the last year, or a graph? Which would help you better understand the behavior of the market? Bicycle drivetrain data is no different.
The challenge is this: suppose we have these two example gearings, 48/12 and 36/12. We want to make some sort of picture that makes it obvious that 1) they're the SAME, because they have the same gear ratio, but also that 2) they're DIFFERENT, because they're a physically different combination of chain and cogs.
The gear ratio itself provides a way out. Imagine that we think of our gear combinations as points on a two-dimensional graph, where one axis represents the front gears and the other axis represents our rear gears:
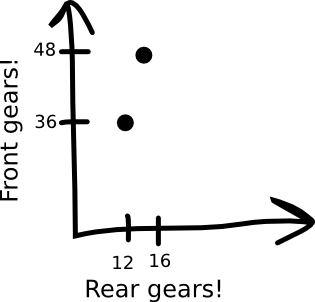
The awesome thing about this graph is that it contains the gear ratio in it! Think about how we measure steepness: sometimes we measure it in degrees (this roof has a 30º pitch), sometimes we measure it as a percentage (10% GRADE NEXT SEVEN MILES), and sometimes we measure it as the change in height per change in length (this pipe drops one foot every 20 feet). If we take our graph, and we draw a line that goes up three units for every one unit it goes over—a line that has a slope of 3—it will hit both our 48/16 combination and our 36/12 combination:
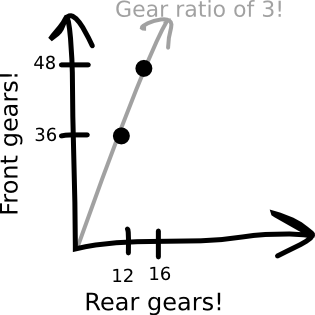
They're two distinct points—so they're different—yet they're lying on the same line—so we can see they're the same! But why stop there? Why not plot your entire drivetrain—why not plot every possible gear combination?
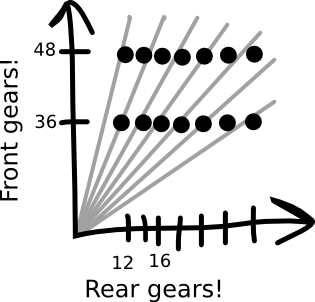
I realized that I could combine two of the minor loves of my life: bicycles and data visualization. I spent a weekend banging out a program to automatically generate these drivetrain graphs. Give it your gears, and it’ll show you not just the gear ratios but also the gear inches, the meters development, and all those other terms I still don't understand! If you tell it your wheel and tire size, it'll even tell you how fast you'll go at a given cadence. And, you can even compare different drivetrains—you can actually SEE, with a picture and not just with numbers, how different gearings will affect your ability to ride hills and flats.
Ultimately I ended up going with the Deore triple—you can see it as one of the default drivetrains on the graph. This was partly due to the graph, and partly due to a grueling, mountainous ride I had taken a few weeks earlier from Palo Alto to Santa Cruz. Oh, and my old gears? Now I have a nice new set of bottle openers, keychains, and coasters:




